viernes, 6 de enero de 2012
Isaac Newton
Científico inglés (Woolsthorpe, Lincolnshire, 1642 - Londres, 1727). Hijo póstumo y prematuro, su madre preparó para él un destino de granjero; pero finalmente se convenció del talento del muchacho y le envió a la Universidad de Cambridge, en donde hubo de trabajar para pagarse los estudios. Allí Newton no destacó especialmente, pero asimiló los conocimientos y principios científicos de mediados del siglo XVII, con las innovaciones introducidas por Galileo, Bacon, Descartes, Kepler y otros.
Tras su graduación en 1665, Isaac Newton se orientó hacia la investigación en Física y Matemáticas, con tal acierto que a los 29 años ya había formulado teorías que señalarían el camino de la ciencia moderna hasta el siglo XX; por entonces ya había obtenido una cátedra en su universidad (1669)
http://www.biografiasyvidas.com/biografia/n/newton.htm
Ley de Hooke
Ley de Hooke (Elasticidad)
Cuando un objeto de somete a fuerzas externas, sufre cambios de tamaño o de forma, o de ambos. Esos cambios dependen del arreglo de los átomos y su enlace en el material.
Cuando un peso jala y estira a otro y cuando sele quita este peso y regresa a su tamaño normal decimos que es un cuerpo elástico.
Elasticidad: Propiedad de cambiar de forma cuando actúa una fuerza de deformación sobre un objeto, y el objeto regresa a su forma original cuando cesa la deformación.
Los materiales no deformables se les llama inhelásticos (arcilla,plastilina y masa de repostería). El plomo también es inhelástico, porque se deforma con facilidad de manera permanente.
Si se estira o se comprime más allá de cierta cantidad, ya no regresa a su estado original, y permanece deformado, a esto se le llama límite elástico.
*Cuando se tira o se estira de lago se dice que está en tensión (largas y delgadas).
*Cuando se aprieta o se comprime algo se dice que está en compresión (cortas y gruesas).
Ley de Hooke:
La cantidad de estiramiento o de compresión (cambio de longitud), es directamente proporcional a la fuerza aplicada.
F=Kx
Principios de la dinamica
Primer principio de la dinámica: principio de la inercia.
Todo cuerpo permanece en estado de reposo o en movimiento rectilíneo y uniforme mientras no actúe sobre él una fuerza neta (varias fuerzas pueden estar actuando sobre un cuerpo, pero si la resultante es nula, no hay fuerza neta).
La inercia es la tendencia de un cuerpo a mantener su estado de reposo o de movimiento.
Una interacción es cualquier mecanismo por el que dos o más cuerpos modifican su estado de reposo o de movimiento. La magnitud que mide cuantitativamente la intensidad de una interacción es la fuerza.
Segundo principio de la dinámica: principio fundamental de la dinámica.
Las fuerzas originan aceleraciones. La relación existente entre las magnitudes de fuerza, masa y aceleración, viene definida por la siguiente ecuación:
F neta = m x a
La aceleración de un cuerpo es proporcional a la fuerza resultante ejercida sobre el mismo, con la misma dirección y sentido que dicha fuerza, e inversamente proporcional a la masa del cuerpo.
a = F/m
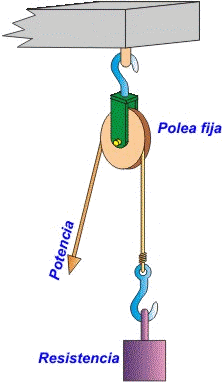
Es el ejemplo de las poleas:
Tercer principio de la dinámica: principio de acción y reacción.
Cuando dos cuerpos interaccionan, las fuerzas que ejercen el uno sobre el otro tienen idéntico módulo y dirección, pero sentidos opuestos.
El tercer principio de la dinámica describe una propiedad importante de las fuerzas: siempre se presentan en parejas.
Las fuerzas de acción y reacción nunca se anulan entre sí, debido a que actúan sobre cuerpos diferentes.
Todo cuerpo permanece en estado de reposo o en movimiento rectilíneo y uniforme mientras no actúe sobre él una fuerza neta (varias fuerzas pueden estar actuando sobre un cuerpo, pero si la resultante es nula, no hay fuerza neta).
La inercia es la tendencia de un cuerpo a mantener su estado de reposo o de movimiento.
Una interacción es cualquier mecanismo por el que dos o más cuerpos modifican su estado de reposo o de movimiento. La magnitud que mide cuantitativamente la intensidad de una interacción es la fuerza.
Segundo principio de la dinámica: principio fundamental de la dinámica.
Las fuerzas originan aceleraciones. La relación existente entre las magnitudes de fuerza, masa y aceleración, viene definida por la siguiente ecuación:
F neta = m x a
La aceleración de un cuerpo es proporcional a la fuerza resultante ejercida sobre el mismo, con la misma dirección y sentido que dicha fuerza, e inversamente proporcional a la masa del cuerpo.
a = F/m
Es el ejemplo de las poleas:
Tercer principio de la dinámica: principio de acción y reacción.
Cuando dos cuerpos interaccionan, las fuerzas que ejercen el uno sobre el otro tienen idéntico módulo y dirección, pero sentidos opuestos.
El tercer principio de la dinámica describe una propiedad importante de las fuerzas: siempre se presentan en parejas.
Las fuerzas de acción y reacción nunca se anulan entre sí, debido a que actúan sobre cuerpos diferentes.
Poleas.
Las poleas son ruedas que tienen el perímetro exterior diseñado especialmente para facilitar el contacto con cuerdas o correas.
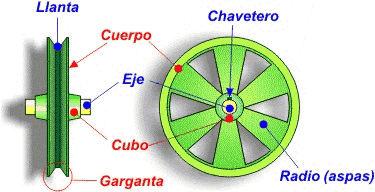
En toda polea se distinguen tres partes: cuerpo, cubo y garganta.
El cuerpo es el elemento que une el cubo con la garganta. En algunos tipos de poleas está formado por radios o aspas para reducir peso y facilitar la ventilación de las máquinas en las que se instalan.
El cubo es la parte central que comprende el agujero, permite aumentar el grosor de la polea para aumentar su estabilidad sobre el eje. Suele incluir un chavetero que facilita la unión de la polea con el eje o árbol (para que ambos giren solidarios).
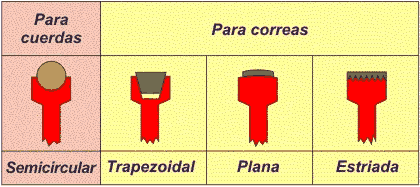
La garganta (o canal ) es la parte que entra en contacto con la cuerda o la correa y está especialmente diseñada para conseguir el mayor agarre posible. La parte más profunda recibe el nombre de llanta. Puede adoptar distintas formas (plana, semicircular, triangular...) pero la más empleada hoy día es la trapezoidal.
Las poleas empleadas para tracción y elevación de cargas tienen el perímetro acanalado en forma de semicírculo (para alojar cuerdas), mientras que las empleadas para la transmisión de movimientos entre ejes suelen tenerlo trapezoidal o plano (en automoción también se emplean correas estriadas y dentadas)
Mas informacion en http://es.wikipedia.org/wiki/Polea
En toda polea se distinguen tres partes: cuerpo, cubo y garganta.
El cuerpo es el elemento que une el cubo con la garganta. En algunos tipos de poleas está formado por radios o aspas para reducir peso y facilitar la ventilación de las máquinas en las que se instalan.
El cubo es la parte central que comprende el agujero, permite aumentar el grosor de la polea para aumentar su estabilidad sobre el eje. Suele incluir un chavetero que facilita la unión de la polea con el eje o árbol (para que ambos giren solidarios).
La garganta (o canal ) es la parte que entra en contacto con la cuerda o la correa y está especialmente diseñada para conseguir el mayor agarre posible. La parte más profunda recibe el nombre de llanta. Puede adoptar distintas formas (plana, semicircular, triangular...) pero la más empleada hoy día es la trapezoidal.
Las poleas empleadas para tracción y elevación de cargas tienen el perímetro acanalado en forma de semicírculo (para alojar cuerdas), mientras que las empleadas para la transmisión de movimientos entre ejes suelen tenerlo trapezoidal o plano (en automoción también se emplean correas estriadas y dentadas)
Mas informacion en http://es.wikipedia.org/wiki/Polea
Vectores.
Características de un vector:
- Intensidad.
- Dirección.
- Sentido.
- Punto de aplicación.
Para conocer la dirección y el sentido del cuerpo, hace falta conocer las fuerzas que actúan sobre él.
Supongamos que la M es el cuerpo.
F.normal
↑
F.rozamiento ← M → F. motor
↓
Peso
Si la fuerza de rozamiento es igual a la fuerza motor el cuerpo no se mueve.
La fuerza normal se anula con el peso del cuerpo.
Fórmula de la fuerza de rozamiento:
F.roz = μ x N
Problema resuelto:
Supongamos que el cuerpo está en una mesa.
- Calcula la fuerza neta del cuerpo.
- Calcula la aceleración.
m = 5 kg
F.roz ← M → 100N
μ = 0,5
g aproximádamente = 10 m/s al cuadrado
F roz = 0,5 x 10 x 5 = 25 N -------> Nota: la fuerza normal es la misma que el peso.
M → 75N
F = m x a
a = 75/5 = 15 m/s al cuadrado
- Intensidad.
- Dirección.
- Sentido.
- Punto de aplicación.
Para conocer la dirección y el sentido del cuerpo, hace falta conocer las fuerzas que actúan sobre él.
Supongamos que la M es el cuerpo.
F.normal
↑
F.rozamiento ← M → F. motor
↓
Peso
Si la fuerza de rozamiento es igual a la fuerza motor el cuerpo no se mueve.
La fuerza normal se anula con el peso del cuerpo.
Fórmula de la fuerza de rozamiento:
F.roz = μ x N
Problema resuelto:
Supongamos que el cuerpo está en una mesa.
- Calcula la fuerza neta del cuerpo.
- Calcula la aceleración.
m = 5 kg
F.roz ← M → 100N
μ = 0,5
g aproximádamente = 10 m/s al cuadrado
F roz = 0,5 x 10 x 5 = 25 N -------> Nota: la fuerza normal es la misma que el peso.
M → 75N
F = m x a
a = 75/5 = 15 m/s al cuadrado
jueves, 5 de enero de 2012
Más allá de la partícula de Dios.
El CERN sienta las bases de la «nueva Física».
Ha cumplido con los objetivos marcados en 2011. Pese a que no han encontrado aún la partícula de Dios, ya se sabe dónde está y cómo buscarla. El próximo paso será elevar la potencia de luminosidad, para aumentar el número de colsiones hasta multiplicarlas por 10 y encontrar las piezas del puzzle que les falta.
Va más allá de conocer esa ansiada pieza del puzzle de la Física, el Bosón de Higgs o la famosa «partícula de Dios». El Gran Colisionador de Hadrones (LCH, por sus siglas en inglés) tiene otros propósitos, como manifiesta Manuel Aguilar, responsable del Proyecto Espectrómetro Magnético Alpha (AMS) del Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas y vicepresidente del Consejo Europeo para la Investigación Nuclear (CERN), «la razón de ser del LHC es explorar las leyes que rigen el microcosmos en una región de energías hasta ahora innacesible y una primera prioridad del programa de investigación era tratar de identificar la partícula del Bosón de Higss, predicha por el Modelo Estándar, o, en su defecto, excluir su existencia. Ambas metas están próximas y, casi con certeza, llegaremos a ellas dentro de un año».
En esta senda, y para llegar a una mayor comprensión de los fenómenos del Universo preven incrementar la luminosidad del LHC en 2020. Si todo va bien, el LHC 2.0 o de «alta luminosidad» estará a pleno rendimiento dentro de ocho o nueve años, gracias a la cooperación de los científicos del CERN y de colegas estadounidenses y japoneses. La actualización permitirá a los operadores llevar a cabo hasta 10 veces más de colisiones respecto a los cientos de ahora, lo que permitirá una visión profunda sobre la composición del Universo.
Gracias a este paso se comprenderá mejor lo que ocurre cuando las partículas colisionan en un acelerador de partículas y se podrá evaluar con mayor exactitud el funcionamiento del LHC. «Éste ya produce una luminosidad más elevada que cualquier otro acelerador de protones de alta energía del mundo», explica el CERN en un comunicado, pero su mejora ayudará a estudiar con más precisión y exactitud los procesos extremadamente raros que suceden en el curso de la colisión de las partículas.
Mas informacion en http://www.larazon.es/noticia/4011-mas-alla-de-la-particula-de-dios-el-cern-sienta-las-bases-de-la-nueva-fisica y en http://www.elmundo.es/elmundo/2011/12/13/ciencia/1323778726.html
Ha cumplido con los objetivos marcados en 2011. Pese a que no han encontrado aún la partícula de Dios, ya se sabe dónde está y cómo buscarla. El próximo paso será elevar la potencia de luminosidad, para aumentar el número de colsiones hasta multiplicarlas por 10 y encontrar las piezas del puzzle que les falta.
Va más allá de conocer esa ansiada pieza del puzzle de la Física, el Bosón de Higgs o la famosa «partícula de Dios». El Gran Colisionador de Hadrones (LCH, por sus siglas en inglés) tiene otros propósitos, como manifiesta Manuel Aguilar, responsable del Proyecto Espectrómetro Magnético Alpha (AMS) del Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas y vicepresidente del Consejo Europeo para la Investigación Nuclear (CERN), «la razón de ser del LHC es explorar las leyes que rigen el microcosmos en una región de energías hasta ahora innacesible y una primera prioridad del programa de investigación era tratar de identificar la partícula del Bosón de Higss, predicha por el Modelo Estándar, o, en su defecto, excluir su existencia. Ambas metas están próximas y, casi con certeza, llegaremos a ellas dentro de un año».
En esta senda, y para llegar a una mayor comprensión de los fenómenos del Universo preven incrementar la luminosidad del LHC en 2020. Si todo va bien, el LHC 2.0 o de «alta luminosidad» estará a pleno rendimiento dentro de ocho o nueve años, gracias a la cooperación de los científicos del CERN y de colegas estadounidenses y japoneses. La actualización permitirá a los operadores llevar a cabo hasta 10 veces más de colisiones respecto a los cientos de ahora, lo que permitirá una visión profunda sobre la composición del Universo.
Gracias a este paso se comprenderá mejor lo que ocurre cuando las partículas colisionan en un acelerador de partículas y se podrá evaluar con mayor exactitud el funcionamiento del LHC. «Éste ya produce una luminosidad más elevada que cualquier otro acelerador de protones de alta energía del mundo», explica el CERN en un comunicado, pero su mejora ayudará a estudiar con más precisión y exactitud los procesos extremadamente raros que suceden en el curso de la colisión de las partículas.
Mas informacion en http://www.larazon.es/noticia/4011-mas-alla-de-la-particula-de-dios-el-cern-sienta-las-bases-de-la-nueva-fisica y en http://www.elmundo.es/elmundo/2011/12/13/ciencia/1323778726.html
lunes, 2 de enero de 2012
Queremos hallar la gravedad que hay en Santoña y para ello necesitamos los siguientes materiales:
2 pelotas que tengan exactamente el mismo peso
Un palo corto
Un palo largo
Varios cronómetros (2 por lo menos)
¿Cómo lo vamos a hallar?
1º: tenemos que hallar una altura concreta (nosotros hemos cogido la de un 2º piso de un edificio).
Para saber cual es la altura aproximada del edificio utilizamos los palos, colocamos el palo largo en un punto concreto y el palo corto paralelo a este.
Tenemos que comprobar que, si miramos desde lo alto del palo pequeño hacia el edificio y cuadren la altura del palo largo con la del 2º piso.
Y si os dais cuenta esto forma un triangulo y la diagonal, es la hipotenusa del triangulo de Tales.
También hay que medir la distancia que hay entre la pared y el palo corto, que es uno de los catetos; el otro cateto es la distancia del 2º piso al suelo.
Palo corto (1,22m)
Palo largo (2,53m)
Si sabemos que la distancia de la pared al suelo son, 8,52m:
2,53-1,22=1,31m
8,58/1,52= 7,34/1,31
7,34+1,22=8,56m
Al ponerlo en común con más gente la media nos ha dado 10,18m
El siguiente paso ha sido tirar unas pelotas desde el 2º piso de dicho edificio, con varios cronómetros hemos cronometrado el tiempo en el que tardan en caer las pelotas, nos a dado un tiempo medio de 1,23s.
Teniendo en cuanta la formula de la gravedad:
g = (2 x vf)/t^2
Lo que nos da como resultado final 13,48 = g.
comparado con la cifra correcta nos da una cota de error del 37%. Un error bastante grande, probablemente debido al calculo erróneo del tiempo que tardan en caer las pelotas por los cronómetros .
2 pelotas que tengan exactamente el mismo peso
Un palo corto
Un palo largo
Varios cronómetros (2 por lo menos)
¿Cómo lo vamos a hallar?
1º: tenemos que hallar una altura concreta (nosotros hemos cogido la de un 2º piso de un edificio).
Para saber cual es la altura aproximada del edificio utilizamos los palos, colocamos el palo largo en un punto concreto y el palo corto paralelo a este.
Tenemos que comprobar que, si miramos desde lo alto del palo pequeño hacia el edificio y cuadren la altura del palo largo con la del 2º piso.
Y si os dais cuenta esto forma un triangulo y la diagonal, es la hipotenusa del triangulo de Tales.
También hay que medir la distancia que hay entre la pared y el palo corto, que es uno de los catetos; el otro cateto es la distancia del 2º piso al suelo.
Palo corto (1,22m)
Palo largo (2,53m)
Si sabemos que la distancia de la pared al suelo son, 8,52m:
2,53-1,22=1,31m
8,58/1,52= 7,34/1,31
7,34+1,22=8,56m
Al ponerlo en común con más gente la media nos ha dado 10,18m
El siguiente paso ha sido tirar unas pelotas desde el 2º piso de dicho edificio, con varios cronómetros hemos cronometrado el tiempo en el que tardan en caer las pelotas, nos a dado un tiempo medio de 1,23s.
Teniendo en cuanta la formula de la gravedad:
g = (2 x vf)/t^2
Lo que nos da como resultado final 13,48 = g.
comparado con la cifra correcta nos da una cota de error del 37%. Un error bastante grande, probablemente debido al calculo erróneo del tiempo que tardan en caer las pelotas por los cronómetros .
Suscribirse a:
Comentarios (Atom)